子どもにおすすめの理系センスを磨く図形ワーク③【小学校受験対策編】

はじめに

この記事を執筆します荒木義明です。敷きつめ模様（テセレーション）の数理を研究する数学者です。数学の研究で見つかる面白い形や模様の楽しさを多くの人に伝えようと、全国の科学館や小学校などで展示やワークショップを行っています。

この記事は、主に未就学児から小学生までのお子さんを対象とした敷きつめ図形を使った楽しいワークをご紹介しています。前回は「数と図形のセンスを磨く編」として、T3パズルを組み合わせてできる柄の種類を数えました。

第3弾となる今回もT3パズルを利用して、より踏み込んで理系のセンスを磨く話題をお届けします。T3パズルとは下図のように上下を2色に塗り分け正三角形の1種類のピースを並べるパズルです。左と右に2つのピースがありますが、これらは同じピースを表面と裏面でそれぞれ置いたものです。左の表面は上が白色、下が緑色です。一方、右の裏面は上が緑色、下が白色です。

タップして拡大

このT3パズルは紙版のピースと、webアプリをご用意しています。webアプリの利用方法の詳細や、紙版のT3パズルの入手方法については、www.t3puzzle.comをご参照ください。

小学校受験の図形問題

さて、今回は「小学校受験の図形問題」の対策に使えるワークを紹介します。小学校受験を目指しているお子さんがいる方は、今まさに図形問題と悪戦苦闘の最中かもしれません。お子さんが小学校受験を経験された方は、図形問題に対する独特のモヤモヤ感を思い出されたでしょうか。

小学校受験の図形問題には、どの受験校でも共通して「数字を使わない」という特徴があります。未修である数字を使う計算問題が小学校受験で出題されることはありません。一方で、抽象的な図形を使った、思考力を試すような良問や珍問が多く出てくるのです。

親御さんの関与の度合いが大きい小学校受験において、家庭学習での問題管理は、親御さんの大きな仕事の一つです。つまづいた問題のプリントをコピーしておき、スラスラ解けるまで繰り返し練習するのです。そのうち、家には大量の問題用紙が溢れるようになります。

同じ問題を繰り返す度に、お子さんが本当に理解しているのか疑心暗鬼になる方もいるでしょう。答えの丸暗記や、偶然の正解でないことを確認するには、類題を解くことが大切です。ただし、ちょうど良い類題を見つけるのは至難の業です。いっそ類題を自作しようかと、モヤモヤした経験がある方もいるかもしれません。

今回紹介するワークでは小学校受験に出題されるような図形問題をT3パズルで作ったものです。問題がT3パズルでできているため、ピースの配置を組み替えるだけで類題を作りやすいメリットがあります。前回のワークで作ったダイヤや六角形を応用して、類題の自作にチャレンジしてみましょう。

図形問題①：同じ図形はどれ？

まず初めに紹介するのは、同じ図形を見つける典型的な図形問題です。お子さんに合わせて、問題文を分かりやすい言葉に言い換えて伝えてください。

この問題の目的は、回転してピッタリ重なる2つの図形を見つけることです。問題を正しく理解するために大切なことは、図形は回転しても元の図形と変わらず同じものだということです。一方で、図形を鏡映しにすると元の図形とは異なるものと区別します。

下の例題では、T3パズルでできた5個のダイヤを比較します。

タップして拡大

この例題の答えが、左から2番目と4番目のダイヤだと、分かったでしょうか？

すぐに答えが見つからなくても心配する必要はありません。このような問題では、ひたむきに取り組む粘り強さが大切です。親御さんも答えの度に一喜一憂せず、お子さんが自分でコツをつかむまで、粘り強く見守ってあげてください。

さて、この例題をひたむきに解くことの大変さを確認しておきましょう。どのダイヤも輪郭だけ見ると、形状も大きさも向きも同じです。また、ダイヤは点対称図形で、輪郭は向きが同じなので、ダイヤ同士を比較するには一方を180度回転することも必要です。5個のダイヤから2個のダイヤを選ぶ組み合わせは10通りなので、回転することも含めて、ダイヤどうしの比較回数が20回必要となる場合があることが分かります。

お子さんがこの例題につまづいた場合は、まずダイヤの数を減らしてチャレンジしてみてください。ダイヤの数が問題の難易度に大きく影響します。1個減らしてダイヤを利用する場合は、4個のダイヤから2個ダイヤを選ぶ組み合わせは6通りと約半分程度に減るのです。

続いて、上の例題の類題を自作してみましょう。この類題でも、T3パズルを2ピース組み合わせたダイヤを使います。前回のワークで確かめた通り、このようなダイヤは36種類あります。これらのダイヤバリエーションの中から5個を上手く選んで、類題を作ります。

この類題を自作する際の注意点は、答えが1つだけになるようにすることです。お子さんの答えと想定する答えが食い違う場合は、類題に複数の答えがある可能性があります。このような失敗を避けるためにも、はじめのうちはシンプルな類題の自作をおすすめします。

次の類題はダイヤを3個だけ使ったよりシンプルなものですが、捻りを入れたものです。

タップして拡大

この類題の答えが、左から1番目と3番目のダイヤだと、分かったでしょうか？

この類題では、ダイヤの数は少ないですが、ダイヤの向きが全て異なるので困惑するかもしれません。まずは、ダイヤどうしを比較する際にダイヤを整列させる必要があります。初めのうちは、ピースを触って実際に整列して問題を解いてみてください。問題に慣れてくるとこの整列が頭の中でできるようになるでしょう。

図形問題②：余分なピースはどれ？

次に紹介するのは、仲間はずれを見つける典型的な図形問題です。お子さんに合わせて、問題文を分かりやすい言葉に言い換えて伝えてください。

この問題の目的は、大きな図形の組み立てに必要ないピースを見つけることです。問題を正しく理解するために大切なことは、図形を組み立てる際に、ピースを動かす方法は平行移動だけで、回転はしないことです。

下の例題では、左側の六角形を組み立てる部品を確認します。

タップして拡大

この例題の答えが、右側の8ピースのうち、左上端のピースと右下端のピースだと、分かったでしょうか？

さて、この例題をひたむきに解くことの大変さを確認しておきましょう。まず組み立てるべき六角形は、上向きのT3パズル3ピースと下向きのT3パズル3ピースを並べたものです。これに対して部品の候補は、上向きのT3パズル4ピースと下向きのT3パズル4ピースと、それぞれ1ピースずつ余分にあります。T3パズル4ピースから3ピースを選ぶ組み合わせは4通りなので、部品6個ごとに比較すると、部品と候補との比較回数が24回必要となる場合があることが分かります。

お子さんがこの例題につまづいた場合は、逆方向から問題にチャレンジしてみてください。つまり、今度は組み立てに必要な部品を見つけるのです。T3パズル4ピースから3ピースを選ぶ組み合わせは4通りなので、部品のいずれかと比較すると、最大4個探せば答えは見つかります。この逆問題の答えをたくさん見つけるうちに、元の問題の答えに辿くでしょう。

この例題についても類題を自作してみましょう。この類題でも、T3パズルを6ピース組み合わせた六角形を使います。前回のワークで確かめた通り、このような六角形は46,656種類あります。これらの六角形のバリエーションの中から1個を選び、さらに余分なピースを2個上手く選びます。

この類題を自作する場合でも、答えが1つだけになることが大切です。ただし、先の問題とは違い、この問題は、類題の自作が容易です。六角形に含まれる上向きのT3パズルと下向きのT3パズルはそれぞれ高々3種類のT3パズルしか利用しないので、それぞれ残り少なくとも3種類ある中から余分なピースを1種類ずつ選べば良いのです。

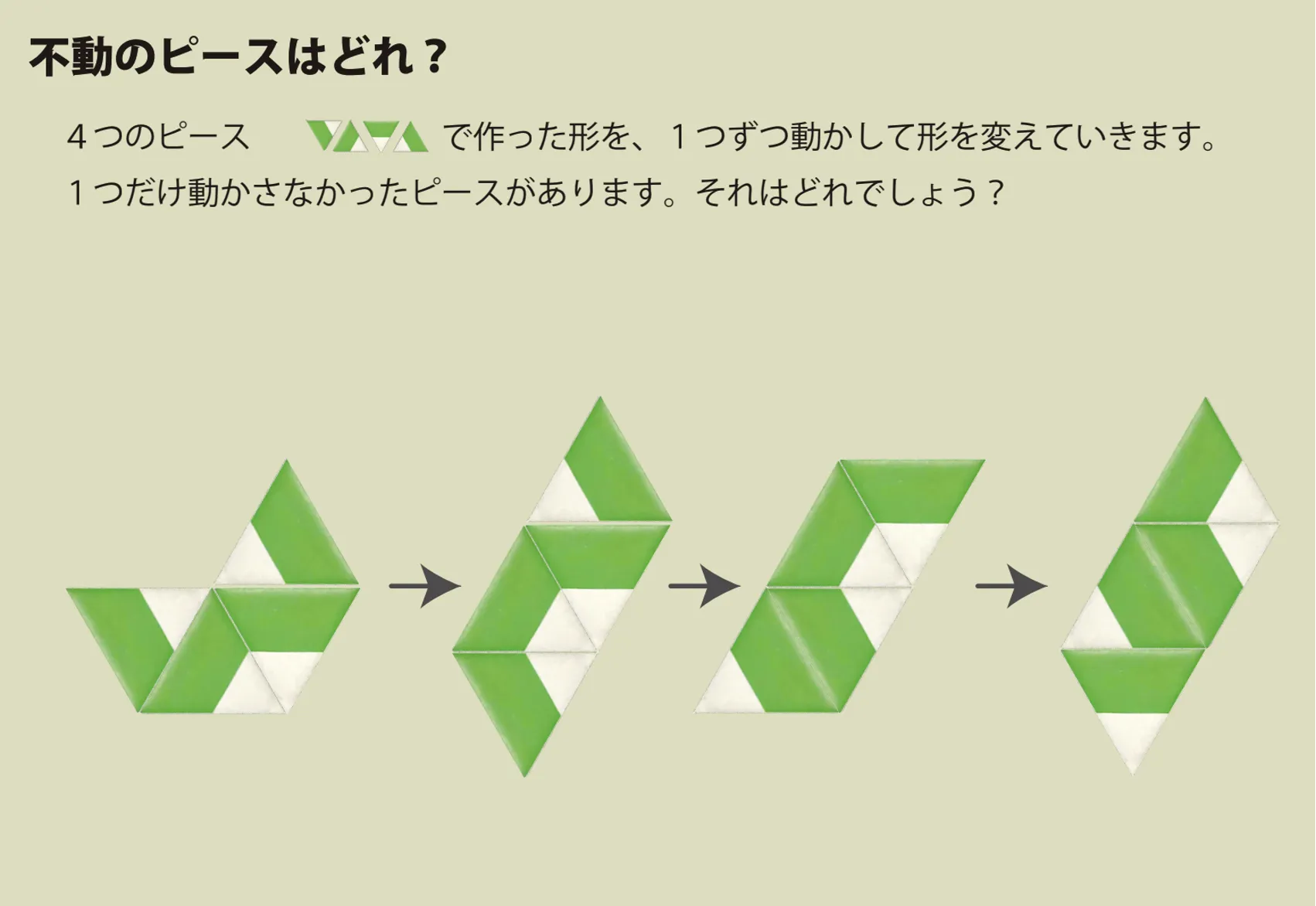
図形問題③：不動のピースはどれ？

最後に紹介するのは、思考力が必要な図形問題の良問です。実際に筆者が類題を自作するきっかけとなった問題です。当時、色々な教材を探しましたが、類題を見つけられず困った末に自作することにしたのです。

この問題の目的は、次々と変形する図形の中で動かないピースを見つけることです。問題を正しく理解するために大切なことは2つあります。1つ目は、変形の度にピースを1個ずつ平行移動することです。2つ目は動かないピースが1つだけということです。

下の例題では、左端の4ピースからなる図形の変形を確認します。

タップして拡大

この例題の答えが、左端図形の下段中央のピースだと、分かったでしょうか？この問題をひたむきに解こうとすると時間がかかるので、じっくり取り組んでください。

この例題をひたむきに解くことの大変さを確認しておきましょう。図形は4ピースからできており変形の度に不動なピースは3個あります。この3個を一つの塊として捉えて、変形の前後で比較して同じ形を見つけます。塊となる3個の選び方は4通りあります。比較の結果、不動の3個でないピースに印をつけます。変形1回あたりこの比較回数は16回、全3回の変形で合計48回必要となる場合があることが分かります。全3回の比較で印をついていないものが、答えとなる不動のピースです。

お子さんがこの例題につまづいた時は、色付きのピースを使ってチャレンジしてみてください。T3パズルのwebアプリではピースに4種類の色を付けることができます。ピースに色が付くことで、変形の前後の不動の3個のピースを1つの塊として認識しやすくなります。

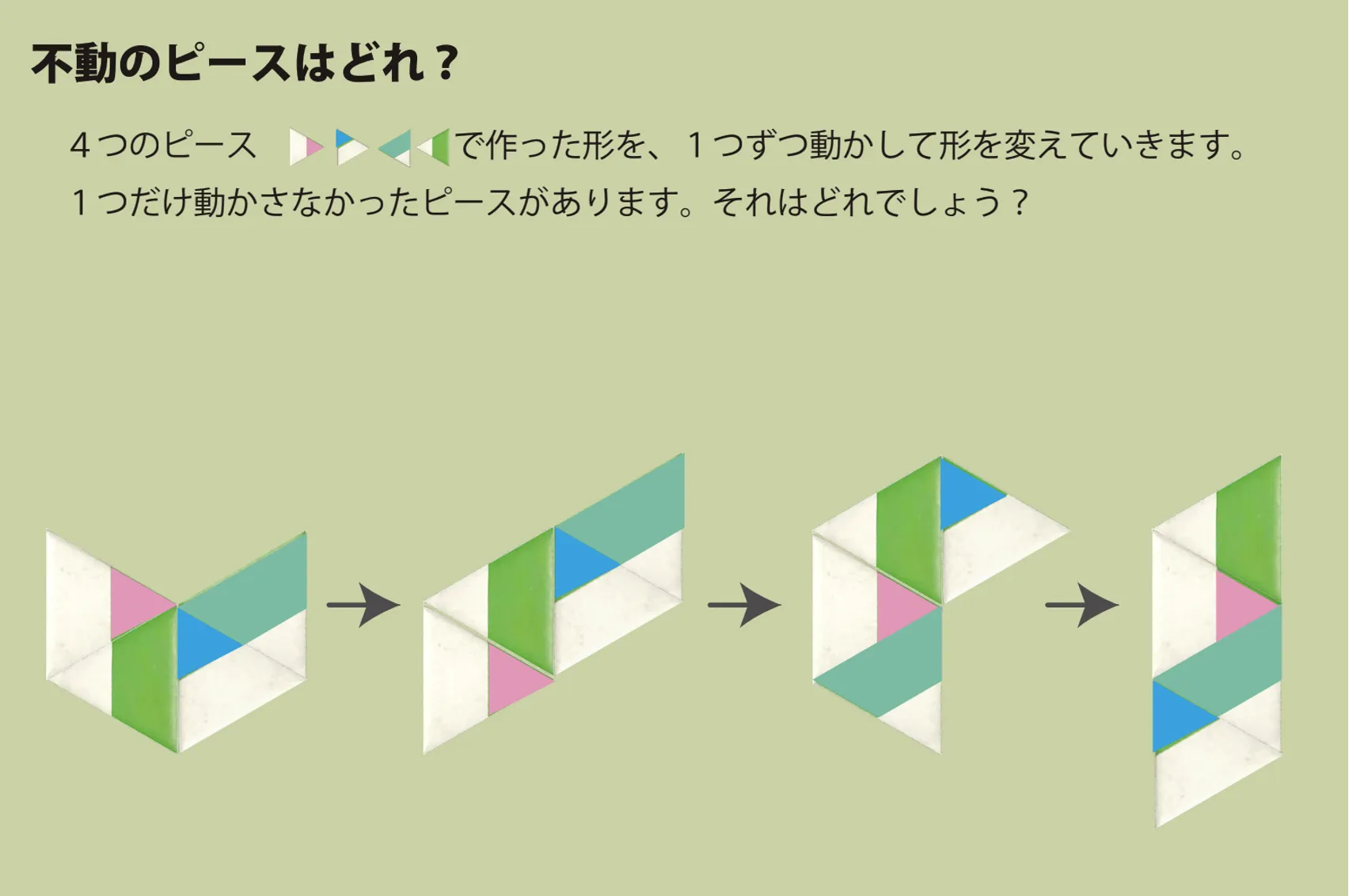
では、この例題についても類題を自作してみましょう。実は、この例題では類題を自作するのはとても容易です。4ピースからなる同じ図形を作り、変形の度に前回とは異なる1ピースを選び、動かせば良いのです。類題を探すより、自作するメリットを実感できるでしょう。

次の類題は色のついたピースを使ったものです。

タップして拡大

この類題の答えが、左端図形の右上のミント色のピースだと、分かったでしょうか？

類題の自作を楽しむ

お子さんが問題に慣れてきたら、今度はお子さんにも類題を自作してもらいましょう。類題を作ることは、問題のより深い理解につながります。自作した類題を親御さんが悩みながら解く姿を見ることが楽しくなるお子さんもいることでしょう。

また、他の典型的な図形問題に対して、T3パズルを使って問題を作るのも良いでしょう。お手持ちの問題用紙の山の中に、自作できそうな問題の心当たりがあるでしょうか。筆者が試したところ、10数種類の典型的な図形問題に対して、T3パズルで問題が作れることを確認しています。

さらに小学校受験の図形問題の枠を超えて、パズルの創作にチャレンジしてみるのはいかがでしょう。今回紹介例題の中でも「不動のピースはどれ？」は、パズル要素の強い問題です。例えばこの発展問題として、「左端の図形から右端の図形への変形に必要な最小の手数でピース移動を見つける」というパズルを考えることもできるでしょう。

この記事のワークを通して、小学校受験の図形問題を楽しく有意義に取り組んでいただければ幸いです。小学校受験に取り組まれているお子さんには「数字を使わない」この時期こそ、図形センスをじっくり育くむチャンスです。また、小学校受験を経験したお子さんには、掴んだ図形センスを掘り起こし、磨きをかけるキッカケにしていただきたいです。

.

画像は全て著者提供

荒木義明

1973年生。慶應義塾大学大学院政策・メディア研究科修了。博士（政策・メディア）。専門は敷きつめ模様（テセレーション）の数理。1998年に日本テセレーションデザイン協会を設立し、国内外の教育機関と連携し敷きつめ模様に関する展示、ワークショップを企画運営。2003年〜2006年東京大学数理科学研究科客員助教授。著書『M.C.エッシャーと楽しむ算数・数学パズル』明治図書(2022)。
（https://www.tessellation.jp/）

荒木義明の記事一覧を見る